As mentioned in a previous post, we simplified the navigation algorithm proposed in this paper.
On large distances, our car drives to a hard-coded GPS point using its GPS module with compass and simple geometrical considerations. But on its way it may encounter obstacles.
Besides two ultrasonic sensors which only prevent the car from hitting anything coming up in front, we mounted a third one on top of a servo motor. This one checks also the surroundings of the car for free passage. To be more specific: it measures in eleven segments and whenever the measurement result is an obstacle closer than two meters, this segment is classified as occupied.
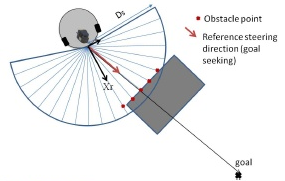
So if there is any obstacle, how does the car decide which way to go? First it groups the free segments together in wide, middle and small gaps. This is important, because it is easier to pass through a large opening than through a small one. In our case, a middle sized gap is exactly three free segements. Wide gaps are any gaps larger and small gaps are any gaps narrower than that.
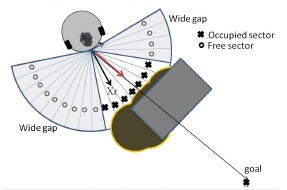
Finally the decision is done through a cost function, which takes two considerations into account for each segment. The further the direction of the segment points away from the goal, the more it leads us away from our objective. We want to find the shortest route. The second cost depends on the gap size. As pointed out above, it is better to drive through large gaps.
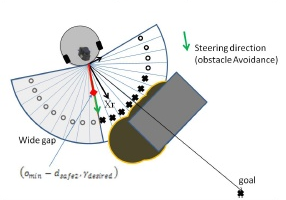
The segment which minimizes the cost function is then choosen as new steering direction and the steering is executed.